Dešifrování hudební geometrie: řešení 70 let starého matematického problému

Jeden z profesorů a jeho spolupracovníci dokázali Polyovu domněnku o vlastních hodnotách disku, což je obtížný problém v matematice.

Dá se tvar bubnu odvodit ze zvuků, které vydává?

Takovou otázku si rád klade Iosif Poltrovic, profesor na katedře matematiky a statistiky na univerzitě v Montrealu. Poltrovic používá spektroskopickou geometrii, odvětví matematiky, k pochopení fyzikálních jevů zahrnujících šíření vln.

Průlom v matematickém odhadu

Loni v létě Poltrović a jeho mezinárodní spolupracovníci – Nikolaj Filonov, Michael Levitin a David Scherr – prokázali zvláštní případ slavné spektroskopické geometrie domněnky, kterou v roce 1954 zformuloval významný maďarsko-americký matematik George Polya.

Odhad se týká odhadu frekvencí kulatého válce nebo, matematicky řečeno, vlastních hodnot disku.

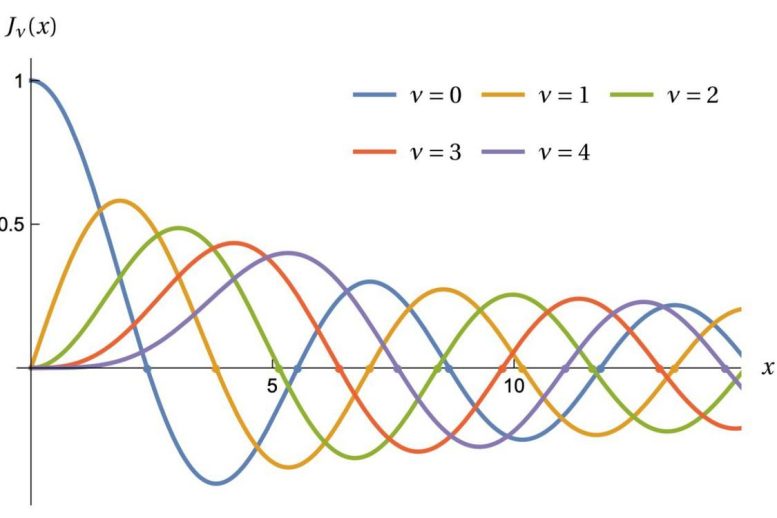
Tento diagram ukazuje Besselovy funkce, kde tečky odpovídají frekvencím zvuků produkovaných kulatým bubnem. Kredit: Michael Levitin

Sám Polya potvrdil svou domněnku v roce 1961 o koulích, které tvoří rovinu, jako jsou trojúhelníky a obdélníky. Do loňského roku byl odhad znám pouze u těchto případů. Disk, i přes svou zdánlivou jednoduchost, zůstal nepolapitelný.

„Představte si nekonečnou podlahu pokrytou dlaždicemi stejného tvaru, které do sebe zapadají a vyplňují prostor,“ řekl Poltrovic. „Mohou být vydlážděny čtverci nebo trojúhelníky, ale ne kotouči. Disky ve skutečnosti nejsou vhodné pro obkládání.“

Univerzálnost a vliv matematiky

V článku publikovaném v červenci 2023 ve sportovním časopise Matematické vynálezyVýzkumníci ukázali, že Bolyova domněnka je pro disk správný, což je případ, který je považován za obzvláště obtížný.

Přestože jejich výsledky mají převážně teoretickou hodnotu, jejich důkazní metoda má aplikace ve výpočetní matematice a numerických výpočtech. Autoři nyní tento přístup zkoumají.

Josef Poltrovič

„Ačkoli je matematika základní věda, v některých ohledech je podobná sportu a umění,“ řekl Poltrovic.

„Pokoušet se dokázat dlouhotrvající domněnku je sport. Najít elegantní řešení je umění. V mnoha případech jsou krásné matematické objevy užitečné, jen musíte najít tu správnou aplikaci.“

Reference: „The Polya Conjecture for Euclidean Spheres“ od Nikolaje Filonova, Michaela Levitina, Iosifa Poltroviče a Davida A. Sdílejte, 5. června 2023, Matematické vynálezy.
doi: 10.1007/s00222-023-01198-1